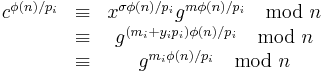Naccache–Stern cryptosystem

Note: this is not to be confused with the Naccache–Stern knapsack cryptosystem.

The Naccache–Stern cryptosystem is a homomorphic public-key cryptosystem whose security rests on the higher residuosity problem. The Naccache–Stern cryptosystem was discovered by David Naccache and Jacques Stern in 1998.

1 Scheme Definition
2 Security
3 References

Scheme Definition

Like many public key cryptosystems, this scheme works in the group 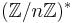$(\mathbb{Z}/n\mathbb{Z})^*$ where n is a product of two large primes. This scheme is homomorphic and hence malleable.

Key Generation

Pick a family of k small distinct primes p₁,...,p_k.
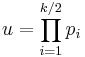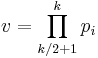Divide the set in half and set $u = \prod_{i=1}^{k/2} p_i$ and $v = \prod_{k/2%2B1}^k p_i$ .
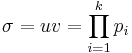
Set $\sigma = uv = \prod_{i=1}^k p_i$
Choose large primes a and b such that both p = 2au+1 and q=2bv+1 are prime.
Set n=pq.
Choose a random g mod n such that g has order φ(n)/4.

The public key is the numbers σ,n,g and the private key is the pair p,q.

When k=1 this is essentially the Benaloh cryptosystem.

Message Encryption

This system allows encryption of a message m in the group 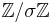$\mathbb{Z}/\sigma\mathbb{Z}$ .

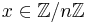Pick a random $x \in \mathbb{Z}/n\mathbb{Z}$ .
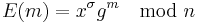
Calculate $E(m) = x^\sigma g^m \mod n$

Then E(m) is an encryption of the message m.

Message Decryption

To decrypt, we first find m mod p_i for each i, and then we apply the Chinese remainder theorem to calculate m mod $\sigma$ .

Given a ciphertext c, to decrypt, we calculate

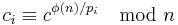$c_i \equiv c^{\phi(n)/p_i} \mod n$ . Thus

$\begin{matrix} c^{\phi(n)/p_i} &\equiv& x^{\sigma \phi(n)/p_i} g^{m\phi(n)/p_i} \mod n\\ &\equiv& g^{(m_i %2B y_ip_i)\phi(n)/p_i} \mod n \\ &\equiv& g^{m_i\phi(n)/p_i} \mod n \end{matrix}$

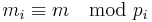where $m_i \equiv m \mod p_i$ .

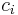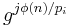Since p_i is chosen to be small, m_i can be recovered be exhaustive search, i.e. by comparing $c_i$ to $g^{j\phi(n)/p_i}$ for j from 1 to p_i-1.
Once m_i is known for each i, m can be recovered by a direct application of the Chinese remainder theorem.

Security

The semantic security of the Naccache–Stern cryptosystem rests on an extension of the quadratic residuosity problem known as the higher residuosity problem.

References

Original paper

Public-key cryptography

Algorithms	Benaloh · Blum–Goldwasser · Cayley–Purser · CEILIDH · Cramer–Shoup · Damgård–Jurik · DH · DSA · EPOC · ECDH · ECDSA · EKE · ElGamal (encryption · signature scheme) · GMR · Goldwasser–Micali · HFE · IES · Lamport · McEliece · Merkle–Hellman · MQV · Naccache–Stern · NTRUEncrypt · NTRUSign · Paillier · Rabin · RSA · Okamoto–Uchiyama · Schnorr · Schmidt–Samoa · SPEKE · SRP · STS · Three-pass protocol · XTR

Theory	Discrete logarithm · Elliptic curve cryptography · RSA problem

Standardization	ANS X9F1 · CRYPTREC · IEEE P1363 · NESSIE · NSA Suite B

Topics	Digital signature · OAEP · Fingerprint · PKI · Web of trust · Key size

Cryptography

History of cryptography · Cryptanalysis · Cryptography portal · Outline of cryptography

Symmetric-key algorithm · Block cipher · Stream cipher · Public-key cryptography · Cryptographic hash function · Message authentication code · Random numbers · Steganography